Optimal Filtering and Residual Analysis in Errors-in-Variables Model Identification

Abstract

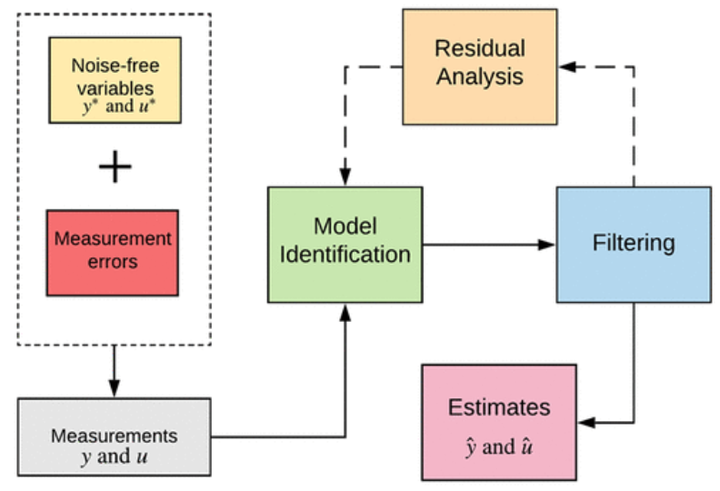
Dynamic model identification from time series data is a critical component of process control, monitoring, and diagnosis. An important adjunct of model identification is the derivation of filtered estimates of the variables and consequent one-step-ahead prediction errors (residuals) which are very useful for model assessment and iterative model identification. In this work, we present an optimal filtering and residual generation method for the errors-in-variables (EIV) scenario, wherein both the input and output variable measurements are contaminated with errors. The main idea is to combine an EIV-identification strategy with the EIV-Kalman filter (EIV-KF) that is known to provide optimal filtered estimates and residuals of both inputs and outputs for a linear dynamical process in the EIV case. In this work, we combine the EIV-KF with the dynamic iterative principal component analysis (DIPCA) approach that has been recently developed for EIV model identification. This work assumes prominence in that the optimally generated residuals are critical to the tasks of model assessment, fault detection, and diagnosis. The use of residuals in model assessment and reidentification is illustrated in this article, while pointing out that the use of DIPCA alone leads to nonunique filtered estimates and hence nonunique residuals. We remark that the proposed method can be used with any other EIV identification technique.