Avatar

Deepak Maurya

PhD Candidate @ CSE Dept

Purdue Unviersity

About Me

I am currently a PhD candidate at CSE Dept, Purdue Unviersity, advised by Prof. Jean Honorio.

Before joining Purdue University, I was an MS (Research) scholar under the guidance of Prof. Balaraman Ravindran and Prof. Shankar Narasimhan at CSE department, IIT Madras. My MS work was focused on spectral hypergraph theory using tensor representation of hypergraphs.

I finished my Dual Degree (B.Tech + M.Tech) in Electrical Engineering from IIT Madras in 2016 where I collaborated with Prof. Arun K. Tangirala, Prof. Shankar Narasimhan for my final year research project. I am also fortunate for the opportunity to closely work with Prof. Raghunathan Rengaswamy, Prof. Manikandan Narayanan, and Prof. Srinivasan Parthasarathy.

Interests

  • Theoretical Machine Learning
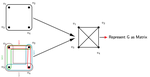
  • Learning on Graphs / Hypergraphs
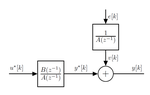
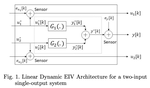
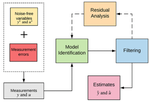
  • System Identification

Education

  • PhD in Computer Science, 2021-Present

    Purdue University

  • MS (Research) in Computer Science, 2018-2021

    Indian Institute of Technology Madras

  • B.Tech and M.Tech in Electrical Engg., 2011-16

    Indian Institute of Technology Madras

News

Publications

Quickly discover relevant content by filtering publications.

ARX Model Identification using Generalized Spectral Decomposition

This article is concerned with the identification of autoregressive with exogenous inputs (ARX) models using spectral decomposition approach. This work is set to appear in 24th International Symposium on Mathematical Theory of Networks and Systems, MTNS 2020
PDF

Incorporating prior knowledge about structural constraints in model identification

Most techniques for model identification do not provide the freedom to incorporate any partial information such as the structure of the model. In this article, we propose model identification techniques which could leverage such partial information to produce better estimates.
PDF

Identification of MISO systems in Minimal Realization Form

The paper is concerned with identifying transfer functions of individual input channels in minimal realization form of a Multi-Input Single Output (MISO) from the inputoutput data corrupted by the error in all the variables.
PDF

Optimal Filtering and Residual Analysis in Errors-in-Variables Model Identification

In this work, we present an optimal filtering and residual generation method for the errors-in-variables (EIV) scenario, wherein both the input and output variable measurements are contaminated with errors.
PDF Code

Hypergraph Partitioning using Tensor Eigenvalue Decomposition

Most of the existing hypergraph partitioning algorithms reduce a hypergraph to graph, which leads to loss of essential information. In this work, we propose a hypergraph partitioning algorithm which does not use reduction step. The work was accepted for a poster presentation in Sets and Partitions workshop in NeurIPS 2019.
PDF Poster

Hyperedge Prediction using Tensor Eigenvalue Decomposition

In this work, we propose a novel algorithm for prediction of new hyperedges using spectral analysis of the Laplacian tensor of hypergraphs. This work was accepted for a poster presentation in Tensor Methods for Emerging Data Science Challenges (TMEDSC) workshop in KDD 2019.
PDF Poster Slides

Identification of Output-Error (OE) Models using Generalized Spectral Decomposition

This article proposes a novel approach for the identification of output-error (OE) models. In this work, we propose a novel two-step non-iterative framework to estimate the delay and order in automated manner using the generalized spectral decomposition. This paper was awarded the best student paper award.
PDF Code Poster Slides

Identification of Errors-in-Variables Models Using Dynamic Iterative Principal Component Analysis

This article proposes a slightly modified and faster version of our identification algorithm for error in variables (EIV) systems presented in this paper.
PDF Code

Identification of Linear Dynamic Systems using Dynamic Iterative Principal Component Analysis

The paper is concerned with identifying models from data that have errors in both outputs and inputs. The proposed algorithm can estimate the order of the system.
PDF Code Slides

Contact