Hypergraph Partitioning using Tensor Eigenvalue Decomposition

Abstract

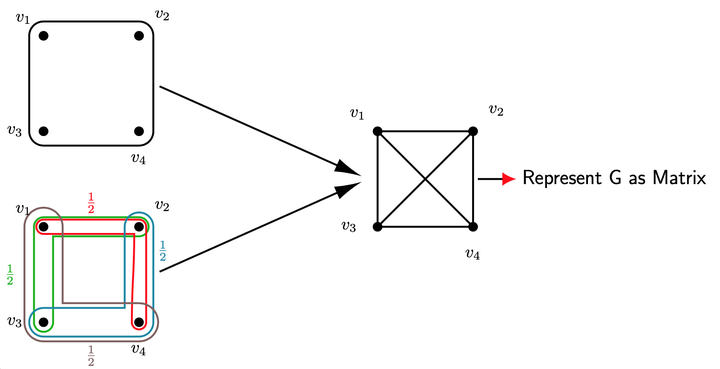
We propose a partitioning algorithm for k-uniform hypergraphs utilizing the tensor-based representation of hypergraphs instead of standard hypergraph-to-graph reduction approaches. This enables us to capture actual super-dyadic interactions instead of dyadic interactions. We extend the notion of minimum ratio-cut and normalized-cut, initially defined on graphs, to hypergraphs and prove that the relaxed optimization problem can be solved using tensor eigenvalue decomposition of hypergraph Laplacian. The efficacy of our method is demonstrated numerically on synthetic hypergraphs.
The work was accepted for a poster presentation in Sets and Partitions workshop in NeurIPS 2019.